Working with big amounts of data requires proper analysis and understanding of the data before implementing it for use. Before deciding on the use of a particular set of data, one needs to first identify its properties and potency. But while analyzing and distributing the data according to their use and properties, there might come some irregularities in the data.

Edureify, the best AI Learning App in the article will provide an insight into Skewness and Kurtosis, the two important tools that help identify the irregularities in the distribution of data. Skewness and Kurtosis identify the asymmetry in the normal distribution of data.

Read on to know more about the same.

Normal Distribution of Data

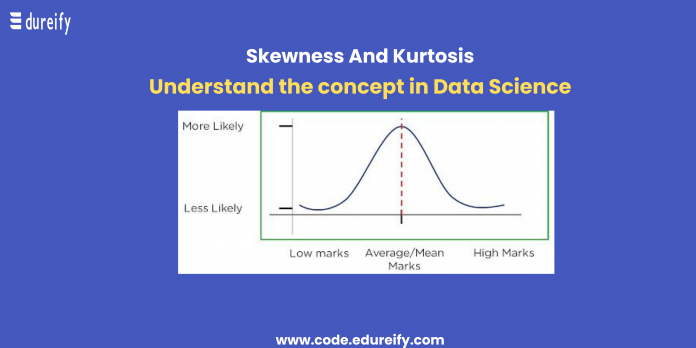
The continued probability of the distribution of a random variable is termed the normal distribution of data. Plotting a random event’s probability provides a probability distribution. A continuous probability distribution is when a random variable has the probability to take any value.

A normal distribution graph has continued infinite probabilities and therefore, when plotted in a graph, has a curved bell shape.

Skewness

While distributing data, it might deviate from the usual. In such a situation, Skewness helps to measure the irregularity in the distribution of data in the graph.

The normal distribution of data has a tilt on one side. This makes the distribution asymmetrical because there happens to be a chance of the data being more or less than the mean.

Types of Skewness

There are two types of Skewness, that is the title on the graph can be of two types-

  • Positively Skewed- When the values in a graph are more tilted on the left side with the right tail spread out, it is a Positively Skewed distribution. In this case, the left-hand side contains more statistical results. Here, the mean, median, and mode always happen to be positive.
  • Negatively Skewed- When the values in a graph are oriented more towards the right side of the distribution, it is Negatively Skewed. In this situation, the mean, median, and mode gets inclined towards the right. Here, the values will always be negative.

Method to Calculate Skewness

The formula of the Skewness is:

Skewness= Mean – Mode/ Standard Deviation

This is also called Pearson’s first coefficient law.

Dividing by the Standard Deviation provides the comparison of the data distribution on the same standard scale.

According to Central Tendency, calculating mode for small amounts of data is not recommended. Hence, to derive a better formula to calculate the Skewness, one can replace the mode with mean and median. Here is how,

We know,

Mode= 3(Median)- 2(Mode)

Therefore now,

Skewness= 3(Mean- Median)/ Standard Deviation

This is also called Pearson’s second coefficient law.

Few key points to note about this calculation-

  • The distribution will be almost symmetrical if the value is between -0.5 and 0.5
  • The data will be negatively skewed if the value is between -1 and -0.5, while the data will be positively skewed if the value is between 0.5 and 1
  • The data becomes highly skewed if the value is less than -1 while negatively skewed and more than 1 while positively skewed

Kurtosis

Edureify had mentioned Outliers in its Range and Interquartile Range article. To identify the presence of outliers in data, one uses Kurtosis. Kurtosis states the degree of the presence of outliers.

A Kurtosis can be understood by observing the curve.

If a curve is flat on the top, like someone had punched it and the tail is heavy, it is Negative Kurtosis. It is also termed Platykurtic.

On the other hand, if the curve is steep on the top and the tail is light, it is Positive Kurtosis. It is also termed Leptokurtic.

Calculating Kurtosis

In a normal distribution, the value of Kurtosis is always 3. This is called Mesokurtic.

When a Kurtosis is greater than 3, it will be Platykurtic. And when a Kurtosis is less than 3, it will be Leptokurtic.

Now, considering the Mesokurtic value is 3, the formula is,

Excess Kurtosis= Kurtosis – 3

 

To conclude, Skewness and Kurtosis are used to get an insight into the spread and height of the normal distribution of data. The fundamental difference between Skewness and Kurtosis is that Skewness is used to denote the horizontal pull in the data and Kurtosis is used to denote the vertical pull in the data.

Interested students who would like to know more about Skewness and Kurtosis of Machine Learning and other tools of Machine Learning can join Edureify’s certified coding courses to learn topics like-

With Edureify’s coding courses, students will also get the benefit of-

  • 200+ learning hours
  • Live lectures with industry experts
  • Access to recorded lectures
  • Doubts cleared instantly
  • Career guidance and access to Edureify’s job portal

So wait no more. Join Edureify’s coding courses and learn from the best.

Some FAQs on Skewness and Kurtosis-

1. What is a normal distribution of data?

The continued probability of the distribution of a random variable is termed the normal distribution of data. Plotting a random event’s probability provides a probability distribution. A continuous probability distribution is when a random variable has the probability to take any value.

2. What is Skewness?

Skewness helps to measure the irregularity in the distribution of data in the graph.

3. What is a formula to measure Skewness?

Skewness= 3(Mean- Median)/ Standard Deviation

4. What is Kurtosis?

To identify the presence of outliers in data, one uses Kurtosis. Kurtosis states the degree of the presence of outliers.

5. From where can I learn more about Skewness and Kurtosis?

Edureify has the best online coding courses that teach about Skewness and Kurtosis.

Facebook Comments