This article will be discussing right angled triangles, area of right triangles, Pythagoras theorem and also Heron’s formula. Let’s start with the basics:

TRIANGLES

Triangles are 3-sided polygons that may or may not be regular, with the special property that the sum of lengths of any two sides of a triangle is greater than the length of the third side. Another important property of triangles is that the sum of the interior angles of all triangles is 180º.

TYPES OF TRIANGLES

Triangles can be categorised based on the values of their sides or their internal angles. For the purpose of this article, we shall stick to the internal-angle based classification. We can put them in the following types:

  1. Acute angle triangle: All 3 interior angles of the triangle are less than 90º.
  2. Obtuse angle triangle: The triangle includes an interior angle greater than 90º.
  3. Right angle triangle: The triangle includes an angle exactly equal to 90º.

RIGHT ANGLE TRIANGLES:

Let us learn more about right angle triangles looking at this image:

                                                             Fig 1.1

One can describe a right triangle in terms of the base, height and hypotenuse. The two sides that are perpendicular to each other are called the BASE and HEIGHT. The side opposite to the 90º angle is the largest side of the triangle, and is called the HYPOTENUSE.

PYTHAGORAS THEOREM:

Famous mathematician Pythagoras came up with a theorem that relates the values of the sides of any right triangle.

As we already know, the sum of any 2 sides of a triangle must be greater than the third side. But we have more information on the sides of right triangles.

According to the Pythagoras theorem, the sum of the squares of the base and height of a triangle equals the square of the hypotenuse of the same triangle.

In mathematical terms:

                                 Base2 + Height2 = Hypotenuse2

Let us look at this theorem in terms of a labelled right angle triangle:

 

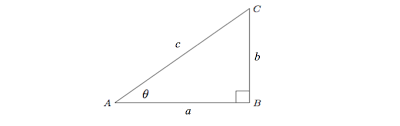
                                                             Fig 1.2

Here  ⦣C=90º , so side c is the hypotenuse. We can take a as the height and b as the base. We may also take the reverse (i.e b as height and a as base), but we will follow conventions according Fig 1.2

Thus, according to the Pythagoras theorem,

                                                 a2 + b2 = c2

AREA OF RIGHT TRIANGLE

1.USING THE UNIVERSAL FORMULA

The universal formula to find the area of a triangle is   A=0.5 * b * h where b is the base length and h is the height of the triangle.

In a right triangle, you need not separately find the height, unlike other triangles. Thus, we can simply multiply the two non-hypotenuse sides and halve that product.

Thus, if we refer to Fig 1.2 we can say that the area of the triangle ABC is:

A= 0.5 * b * c

2.USING HERON’s FORMULA

Heron’s formula is also a universal formula to find the area of a triangle using just the values of the sides, without needing to find the height. If you know the value of all the sides of a triangle, you need not find the height to find the area. You can simply use the Heron formula, which is as follows:

                  Area (A)=√((s)(s-a)(s-b)(s-c))

Where:

s: semiperimeter, i.e (a+b+c) *0.5

a,b,c: sides of the right triangle

Thus, by knowing either all the sides of a triangle, or any 2 sides, we can find the area of the triangle using a combination of Pythagoras theorem and Heron formula or the universal 0.5bh formula to find the area of the triangle.

NOTE:

We can use the universal 0.5bh formula even with the hypotenuse if we know the value of the perpendicular to the hypotenuse from the 90º vertex.

Thus, referring to Fig 1.2, suppose there is a perpendicular from C to c called CD, the area of triangle ABC can also be found as 0.5 * CD * c

For more such articles and notes on geometry, visit www.edureify.com today! 

Facebook Comments